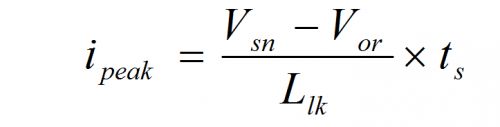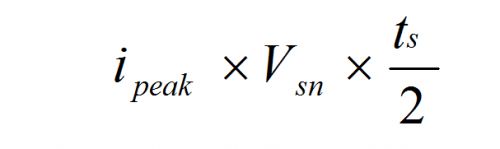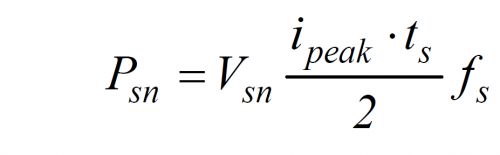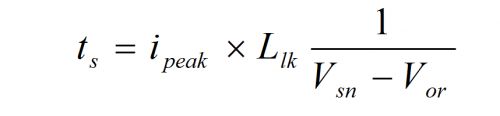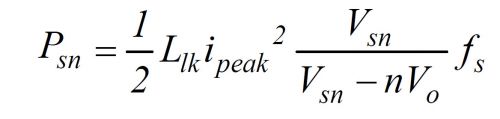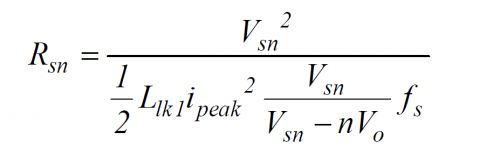RCD 的计算结果为何与实验参数出入很大
不时有网友提到 RCD 的计算问题。有关 RCD 的计算和实验的帖子在坛子里也很有人气。
其中老梁头 的关于反激RCD的实验 中的介绍很详实，是很有价值的一手实验数据。读过帖子之后，给人感觉好像自己亲手做了个实验，受益匪浅。然而，帖子中计算的 RCD 数值和实验得到的参数并不一样（老梁在帖子中的计算过程正确、结果有误）。相信很多网友都有这样的体会 - 就是计算出的电阻 Rsn 比实际实验得到的数值要小很多。大家有没有兴趣讨论一下 ~
（本图摘自Fairchild AN-4147） 
下面介绍一下本人在实验过程中发现的 3个原因 ~
1. 漏感测量的误差大 - 由于仪器和测试的问题导致漏感测量的误差可以很大（尤其是体积小变压器），通常是测得的漏感偏大。导致计算结果的不准确（电阻偏小）。
2. RCD计算公式中忽略了二极管Dsn的正向导通延迟时间和开关损耗，假设所有漏感引起的功耗都消耗在了电阻 Rsn 上，使得计算出的电阻数值偏小。
3. 计算公式忽略了漏感对 MOS管输出电容 Coss 的充电，而这一部分的能量是不能忽略不计的。
看到有网友不太清楚 Rsn 计算公式的推导，顺便在这儿推导一下 ~
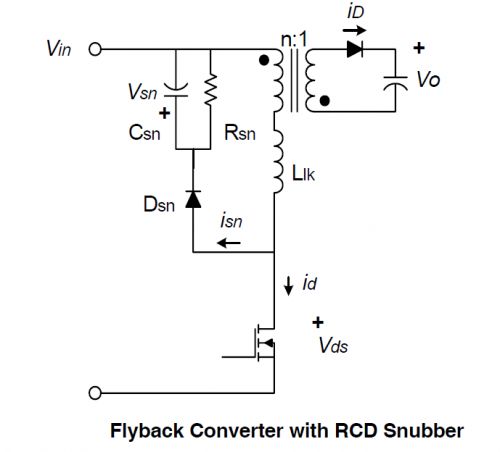
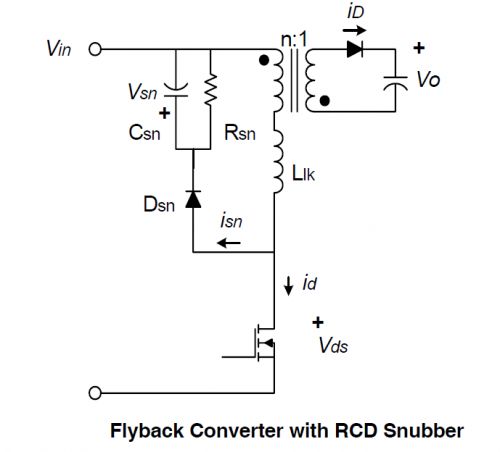
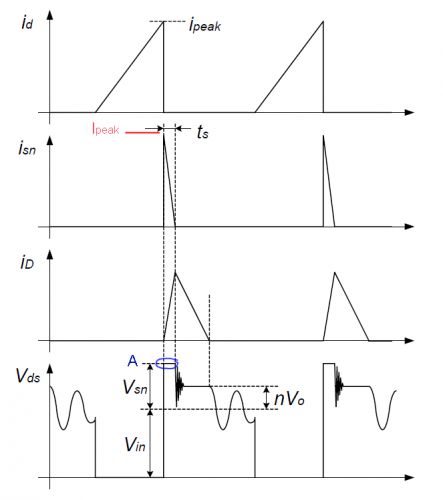
1. 当MOS管关断时，初级电流达到了最大值 Ipeak。电压Vds 迅速上升至A点，漏感 Llk上的能量开始对Csn冲电。
2. Csn上的电压在整个过程中几乎不变，其大小是Vsn。
3. 由于此时次级的整流管已经导通，次级圈上的电压被钳制到输出电压 Vo。反射电压 Vor (或者写成 nVo) 在初级建立。
4. 漏感对 Csn 放电时，漏感上的电压被钳制到 Vsn - Vor。
5. 漏感上的电流变化为
6. 在漏感对Csn充电的过程 ts 中，漏感两端的电压始终是 Vsn - Vor。
7. 充电电流 isn 由初始值 Ipeak 一路线性下降到 0，此时漏感上的能量全部释放掉了。
8. 由于电流 isn 的变化是线性的，可以用几何的方法计算出 Csn 在一个周期里充电的总能量是
9. RCD 线路消耗的功率是
由
得到下面的公式
10. 假设 Csn 在放电的过程中，两端电压变化不大，其值为Vsn。则Rsn近似为
